A Note on the Geometric Organization of Prime Numbers
The distribution of prime numbers has long been characterized by a tension between local erraticism and global regularity. While the Prime Number Theorem provides a smooth asymptotic for their density, the precise “jitter” of individual primes, the gaps between them, is typically treated as a stochastic process.
However, by applying the machinery of exceptional Lie algebras (E₈ and F₄) to the sequence of prime gaps, a different picture emerges. When prime numbers are mapped into these high-dimensional lattices and projected back onto a two-dimensional coordinate system, they appear to organize into a coherent, periodic standing wave.
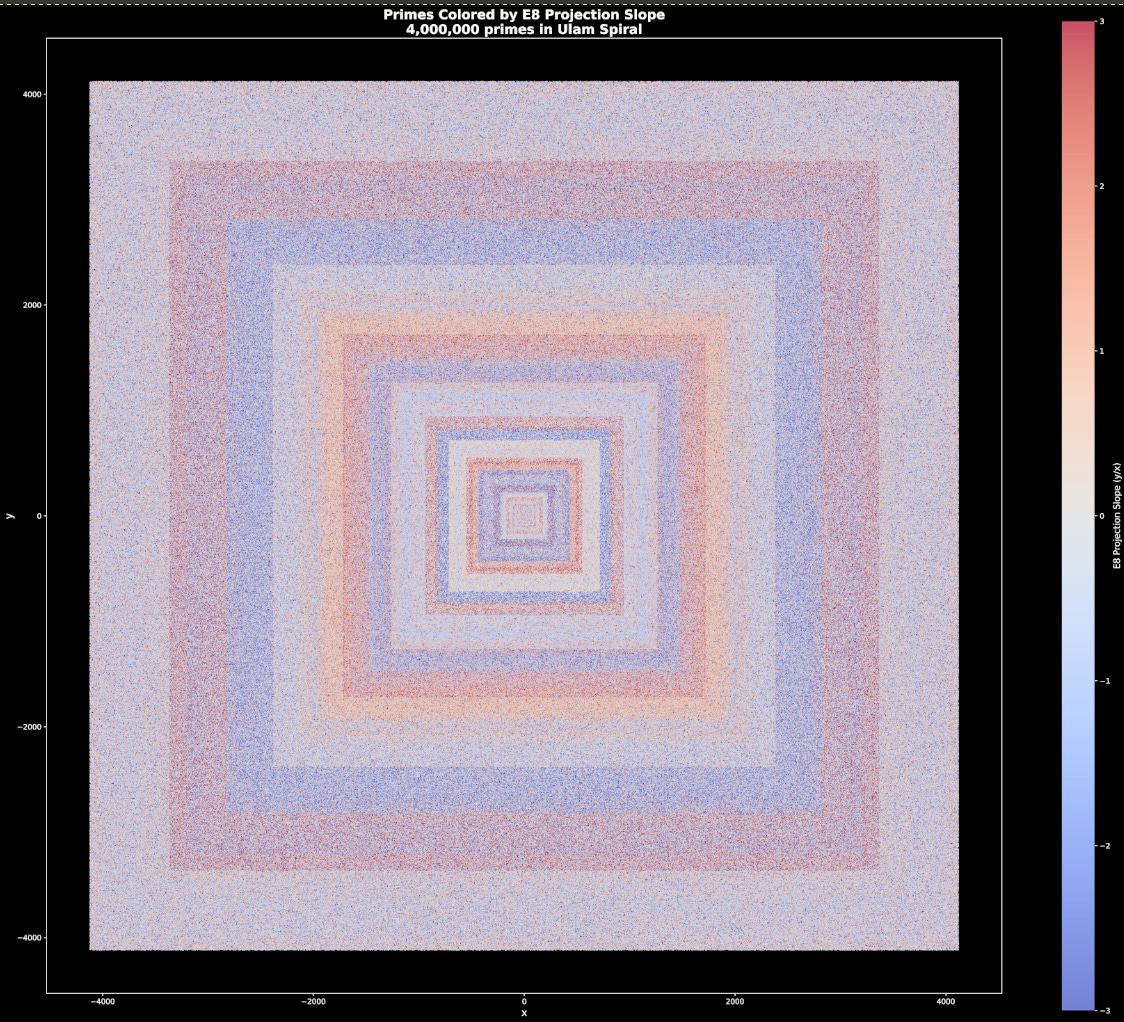
The E₈ Projection
The process begins by taking the first 50 million primes and calculating their normalized gaps—adjusting the raw distance between primes by the local density (𝑙n pₙ). These normalized gaps are then embedded into the E₈ root lattice, an 8-dimensional structure consisting of 240 unit vectors.
By assigning each prime to an E₈ root based on its “arithmetic phase” and projecting that 8D information down to a 2D slope, we can color the primes within a standard Ulam spiral. The result is shown below:
In a random distribution, one would expect a “salt and pepper” noise pattern. Instead, we observe distinct, concentric square rings. These bands of color indicate that the phase of the prime gaps is not independent; rather, it evolves coherently as a function of prime magnitude. This suggests that the “noise” in the prime distribution is actually a holographic signal tuned to a global frequency.
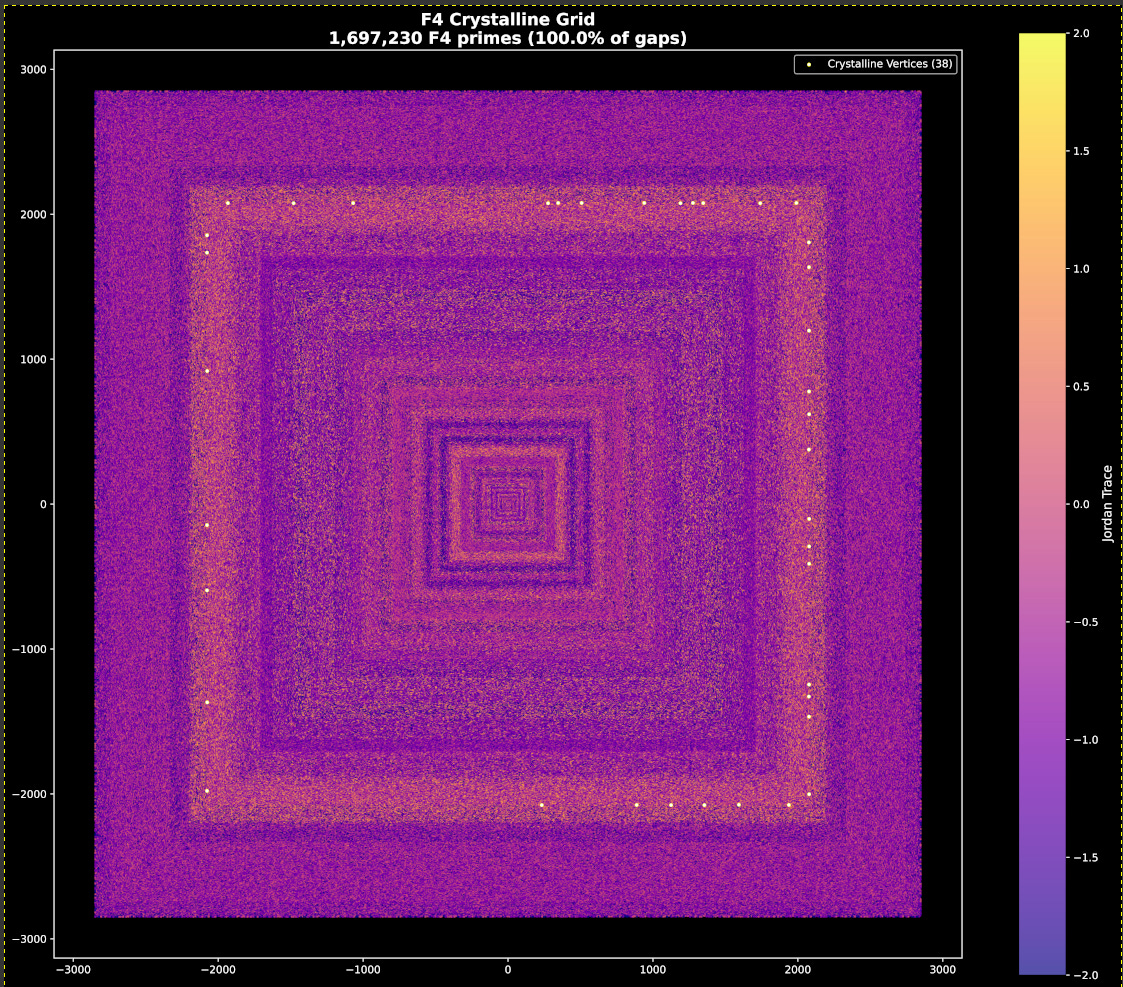
The F₄ Crystalline Skeleton
To look deeper into the “internal logic” of this wave, we can refine the filter. The E₈ lattice contains a maximal sublattice, F₄, which is the automorphism group of the Albert algebra, the unique exceptional Jordan algebra.
By filtering the signal for “projection quality”—essentially looking for primes that resonate most strongly with the F₄ core. the continuous wave resolves into a discrete skeleton.
The bright white points, which we term “Crystalline Vertices,” cluster along the edges and diagonals of the spiral. Empirical analysis of these vertices reveals a specific arithmetic signature: they are exclusively “sexy primes” (primes with a gap of 6) that possess a nilpotent Jordan character.
In the language of dynamical systems, these vertices appear to be the “saddle points” of the arithmetic flow. They form the rigid frame upon which the rest of the prime distribution is draped.
Theoretical Implications: The Hodge–de Rham Diamond
This geometric organization is consistent with a framework we term the Hodge–de Rham Diamond. In this view, the primes are not merely a sequence of integers, but the “Machine Code” of a bulk manifold whose stability is governed by exceptional symmetry.
The mequation of this framework suggests that the Riemann Hypothesis is a requirement for the spectral stability of this Diamond. The critical line (𝜎 = 1/2) acts as the unique axis of transcendental self-duality. If a zero were to exist off this line, the E₈ symmetry observed in these visualizations would break, and the concentric rings would decohere into noise.
Conclusion
The visual evidence suggests that the primes “know” about E₈. Whether this structure is a fundamental property of the integers or a byproduct of the embedding remains a subject for further investigation. However, the transition from the continuous E₈ wave to the discrete F₄ skeleton provides a new, empirical path for examining the relationship between number theory and exceptional geometry.
For those interested in reproducing these results or examining the underlying logic, the complete Python implementation and the formal manuscripts have been made available for public scrutiny.
Data and Code:[github.com/johnjanik/HodgedeRham
and you can find the primes here.
*John A. Janik is a researcher exploring the intersections of differential geometry, exceptional algebras, and number theory, and whatever happens to be on my mind.